본 게시글의 코드는 https://wikidocs.net/22881 를 참고했음을 밝힙니다.

선형 회귀 알고리즘이 공부한 시간에 따라 변하는 성적, 역까지의 거리에 따라 달라지는 집값 등의 수치를 분석하고 예측하는 알고리즘이었다면, 로지스틱 회귀는 점수가 주어질 때 합격인지 불합격인지, 또는 어떤 메일이 스팸 메일인지 정상 메일인지를 구분하는지와 같은 분류 알고리즘이다. 이렇게 둘 중 하나를 결정하는 문제를 이진 분류(Binary Classification)이라 하고, 셋 이상이면 다중 분류(Multiclass Classification)이라 한다. 다중 분류는 다른 회귀 분석 방법이므로 우선은 넘어가자.

이진 분류

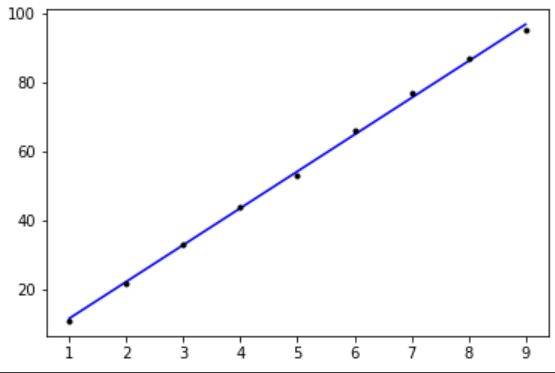
이진 분류 문제는 직선으로 나타내는 것이 적절하지 않다는 것은 아래 그래프만 봐도 알 수 있다.

출처:https://wikidocs.net/22881
합격을 1, 불합격을 0이라 하고 55점까지는 불합격, 60점부터는 합격이라는 것을 도식화한 것이다. 누가 봐도 직선은 아니다. 애초에 직선으로 도식화하기 불가능하다. 분류 문제는 그래서 선형 회귀 분석 방법을 쓰지 못한다. 또, 직선의 경우 음의 무한대부터 양의 무한대와 같은 값도 갖기 때문에 분류 문제에 적합하지 않다.
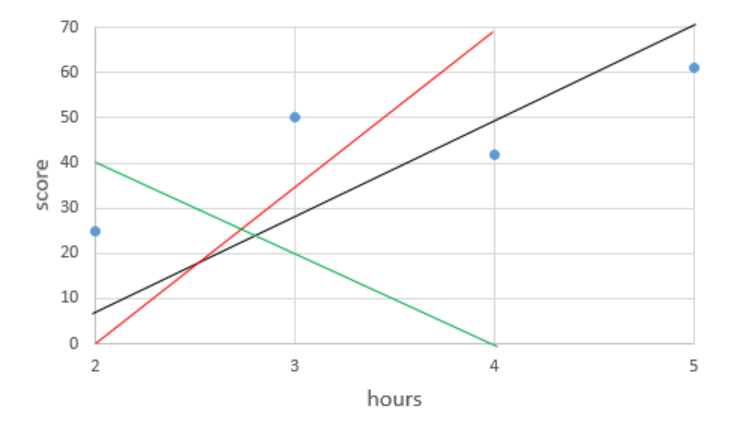
근데 위와 같은 그래프의 경우는, 직선은 아니나 선형함수의 형태로 그래프가 그려져 있는데 이러면 분류 작업이 제대로 작동하지 않는다.(왜 그런지는 딥러닝 챕터: 활성화 함수에서 후술)
따라서, 이러한 직선 형태를 s자 모양의 곡선 형태로 바꾸어주어야 하는데, 이를 시그모이드 함수(Sigmoid Function)이라고 한다.

시그모이드 함수

출처:https://wikidocs.net/22881
출력이 0과 1의 값을 가지면서 곡선 형태를 갖는 함수이다.
저 그림 그대로 출력하는 코드는 아래와 같다.

7번째 줄과 11번째 줄 왜 저렇게 되는지 모르겠지만 일단 코드는 이렇다.
시그모이드 함수도 선형 회귀와 마찬가지로 적합한 w,b값을 찾아내는 것이 목적이다. 그렇다면 가중치 w와 b에 따라 시그모이드 기본 형태가 어떻게 달라지는지를 살펴보고, 그것을 구현하는 코드는 어떻게 되어있는지 살펴보자.

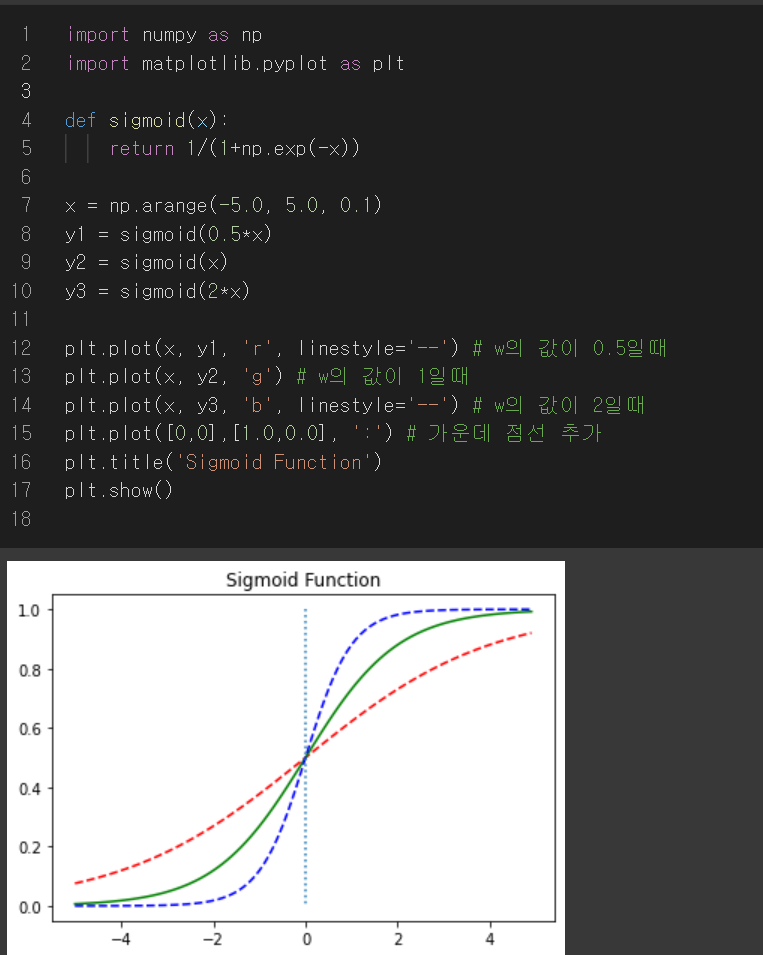
w값이 달라짐에 따라 시그모이드 함수의 경사가 달라지며, 코드는 위와 같이 변경한다. 빨간 점선이 8,12번째 줄, 초록 선(기본형)이 9,13번째, 파란 점선이 10,14번째 줄에 대응이 된다. 위 결과를 보고 w값이 커질수록 경사가 커지고, w값이 작아질수록 경사도 작아짐을 알 수가 있다.

이번에는 b값이 달라짐에 따라 시그모이드 함수가 y축 방향으로 이동하는 것을 볼 수 있다.
w와 b의 값에 따라 시그모이드 기본형 함수에서의 결과와 전혀 다른 결과가 도출되므로 적절한 w,b의 값을 찾는 것이 아주 중요하다
시그모이드 함수는 입력값이 커질수록 1에 수렴, 입력값이 작아질수록 0에 수렴한다. 0.5이상이면 1, 그 이하면 0으로 간주했을 때 0과 1로 분류(즉, 이진 분류)가 되기 때문에 이진 분류 문제를 풀 수 있는 것이다.

이 코드는 제가 학습하면서 참고했던 https://wikidocs.net/111472 예제 코드임을 밝힙니다.

오타가 났다! SGD인데! 참고로 Stochastic Gradient Descent: 배치가 1인 경사 하강법(확률적 경사하강법)이라는 뜻인데, 배치는 지금 알아둘 필요는 없고 나중에 딥러닝 챕터에서 자세히 소개할 것이다.

참고로 위 코드를 실행하면?

위와 같은 결과가 나온다! 보다시피 epoch(에포크라고 하는데 이것도 딥러닝 챕터에서 배치와 같이 설명할 예정이다) 횟수가 많아질수록 cost의 값이 점차 0에 가까워짐을 확인할 수 있다! 이 말인 즉슨, 경사하강법을 통해 0에 가까운 손실을 최소화하는 최적의 값으로 올바르게 찾아가고 있다는 것이다.
그럼, 위에서 임의로 설정한 x_test값을 가설함수에 넣어 예측값을 출력해보면?

위와 같은 결과가 나왔다!

최적화 알고리즘

선형 회귀를 포함한 기계 학습은 결국 비용 함수를 최소화하는 매개 변수인 x와 y을 찾는 것이 목적이다. 이때 사용되는 알고리즘을 최적화 알고리즘(Optimizer)이라고 한다.

- 경사하강법

지난 게시글을 보면 알 수 있듯, 기울기가 너무 커져도, 기울기가 너무 작아져 음수가 되어도 오차는 커진다. 이 오차와 기울기의 관계를 그래프로 나타냈을 때,

출처ㅣhttps://wikidocs.net/21670

비용함수의 값 cost가 가장 낮은 지점은 그래프에서 보면 알다시피 기울기가 0이 되는 지점이다. 바로 이 지점이 우리가 도달해야 할 지점인 것이다. 그리고 그 지점의 w의 값이 우리가 찾는 최적의 w값이 될 것이다. 이 지점보다 위에 있다면 무조건 손실이 그보다 커질 것이다. 따라서 경사를 하강하며 점차 아래로 내려오도록 하여, 최적의 w값에 가까워지도록 하는 것이다. 아래 그림처럼 말이다.

출처ㅣhttps://wikidocs.net/21670
바로 이것을 경사하강법이라고 한다. 경사하강법은 최적화 알고리즘 중에 하나이다. 선형 회귀에서는 경사하강법이 회적화 알고리즘으로 자주 사용된다.

접선의 기울기가 0, 즉 미분값이 0이 되게 하는 값. 그것을 알기 위해 당연히 미분을 해야 한다. 일반적인 공식을 생각해보면 w와 b라는 두개의 매개변수(parameter)가 있기 때문에, 어느 한 쪽만 미분하는 편미분을 이용한다. 기울기는 w와 마찬가지이므로 w에 대해 편미분을 하면 δcost(w)/δw가 될 것이다.
그런데 여기서 끝나는 것이 아니다. 우리는 편미분에서 끝날 게 아니라 이 값을 0에 가깝게 만들어줘야 한다. 그렇게 하기 위해 다음의 공식을 이용한다.

현재 w값에서, 현재 w에서의 접선의 기울기와 학습률을 곱한 값을 뺀 값을, 새로운 w의 값으로 한다는 것을 의미한다.
왜 이러한 식이 도출되었는가를 이해하려면 다음의 그래프를 보자.

상술하기 이전에, 알파 값은 학습률(Learning rate)라는 것인데, 이는 딥러닝 챕터에서 자세히 상술할 터이니 여기서는 신경쓰지 않도록 한다.

w에 대해 미분한 값이 음수라면, 위 공식에 대입해 보았을 때 (-)*(-)가 되고 이는 결국 +가 되는 것이다. 따라서 w는 증가하여 현재 위치보다 오른쪽, 즉 -에서 0에 가까워지는 방향으로 이동할 것이다.
반대로 w대 대해 미분한 값이 양수라면, w값이 감소, +에서 0에 가까워지는 방향으로 이동하므로, 결과적으로 둘 다 모두 접선의 기울기가 0, 즉 cost값이 최소가 되는 값을 찾게 되는 것이다.
실제로 경사하강법은 w뿐 아니라 b에도 적용이 되어 둘 다 경사하강법을 통해 최적의 값을 찾아가게 된다.

이전 게시글에 비용함수, 손실함수, 목적함수에 대해 다뤘는데, 이번에는 저번 게시글에 언급했듯 비용함수, 그중에서도 MSE에 대해 정리하고자 한다.

• MSE란 무엇인가
  Mean Squared Error의 약자로, 평균 제곱 오차라는 뜻이다. 그러니까 수식으로 나타내면
  출처:https://wikidocs.net/21670
  cost는 비용함수, w와 b는 우리가 최적의 결과를 내도록 구해야 하는 값(사람이 임의로 수정할 수 없음. 수정 할 수 있는 것은 하이퍼파라미터라고 불리는 학습률, 에포크 등이 해당)값이다. w와 b에 의해 비용함수가 정의되므로 cost(w,b)와 같이 나타낸다
  그리고 그 옆의 수식이 바로 MSE, 평균 제곱 오차인 것이다. 이전 게시글에 언급했듯 Σ 를 쓰기에 손실함수가 아닌 비용함수로 보는 게 적합하다.
• 왜 회귀에서 MSE를 쓰는가
  MSE등의 비용함수는 단순히 예측값과 실측값의 오차가 아니라 그 오차를 최적화하는 값이 되어야 한다. 세상에는 다양한 문제가 있고, 각 문제의 유형에 따라 가장 적절한 비용 함수를 써야 하는데 회귀 문제에서는 주로 MSE가 쓰인다고 한다. 이 외에 평균 절대 오차 MAE(Mean Absolute Error)도 쓰이는데, 오차들의 제곱이 아닌 오차들의 절댓값의 평균을 의미한다. 이것 또한 나중에 자세히 설명할 때가 올 것이다.
  
  위 그림에서 화살표에 해당하는 것이 오차라고 보면 되는데, 이 오차값이 보다시피 양수일수도, 음수일수도 있다. 양수일땐 상관 없지만, 음수가 있기 때문에 제곱하거나 절댓값을 씌우는 것이다.
• 그럼 이런 비용함수는 왜 쓰는가?
  상술했듯이 기계는 완벽하지 않기 때문에 오차가 나기 마련이다. 대표적으로 회귀의 예시를 들어 MSE, MAE를 비용함수로 써서 처음에 기계가 낸 오차의 평균을 구하고, 이 값을 점점 줄여 나가서 모델의 정확도를 높이는 것이 우리의 목표이기 때문이다. 회귀문제가 아니라면 다른 적절한 비용함수를 쓴다. 이것은 아마 딥러닝 파트에서 다시 설명할 듯 하다.

결론적으로, 우리는 평균 오차값을 최소한으로 만드는 적절한 직선, 즉 minimize cost(w,b)를 찾아내야 하는데, 이 w,b값을 찾아내려면 평균 오차의 값을 찾는 것이 선행되어야 한다. 오차가 클수록 평균오차도 당연히 커질 것이고, 적절한 w,b의 값을 찾아내야 비로소 평균오차의 값이 작아져 적합한 모델이 만들어졌음을 수치로 확인할 수 있기 때문이다. 이 때문에 평균오차의 값을 구해주는 손실함수를 쓰는 것이다.

비용함수에 대해 공부하기 전에, 목적함수와 비용함수, 손실함수 용어가
혼용되어 쓰이고 있다는 것을 알았고 더 조사해 본 결과 엄밀히 따지면 다르다는 것을 알게 되어 더 정리해 보고자 글을 쓰게 되었다.

• 목적함수(Objective Function)
  목적 함수는 말그대로 어떠한 목적을 가지고 모델을 학습해 최적화하고자 하는 함수이다. 일반적으로 딥러닝에서는 경사 하강법(Gradient Descent) 방식을 사용하여 최적화하기 때문에 비용 함수가 바로 목적 함수가 된다. 하지만 MLE(Maximum Likelihood Estimate)와 같이 확률을 최대로 하는 방법을 사용할 경우에 감소하는 방식이 아닌 최대로 하는 방법을 할 때는 비용 함수가 아닌 목적 함수로 언급해야 한다. (출처: https://ok-lab.tistory.com/171)
  MLE가 정확히 기계학습과 무슨 관계가 있는지 모르겠지만 어떤 강의에서 언급된 것을 본 적이 있기 때문에, 이부분은 더 자세히 알아봐야겠다.
• 비용함수(Cost Function)
  비용함수는 더 일반적이다. 어떤 모델의 페널티의 복잡성을 줄이는것(regularization*)과 트레이닝 셋에 전반적인 손실 함수의 총합이 될수도 있다.
  좀 더 자세히 설명하면 예측값과 실제값의 차이가 줄어들수록 더 우리는 많은 값들을 예측할 가능성이 늘어나는데 이 코스트 펑션은 그 차이를 표현하니까 코스트 펑션이 줄어들수록 더 정확한 예측이 가능하다. underfit은 트레이닝이 부족할때 나타난다. underfit은 high bias, high variance의 결과를 가져오는 경우가 많다. low bias, high variance인 overfit이 되어도 문제인데, 트레이닝 셋에만 맞는 값들이 예측되어 bias는 낮지만 실제 미래에 있을 값들이나 새로운 값들에는 맞지 않을 수 있기 때문에 주의해야한다. low bias, low variance인 코스트 펑션을 찾는것이 중요하다.
  에러함수에서 fit이 너무 되면 추가적으로 페널티를 줘서 overfitting도 막아주고 하는 함수를 튜닝하는 테크닉이라 생각하면 좋을 것 같다.

Mean Squared Error MSE(θ)=1N∑Ni=1(f(xi|θ)−yi)2
SVM cost function SVM(θ)=∥θ∥2+C∑Ni=1ξi (there are additional constraints connecting ξi with C and with training set)
regularization in machine learning? 계수의 제약이나 계수의 규약 혹은 계수가 0으로 줄어드는 회귀의 형식같은것이다. 다른말로는 오버피팅의 위험성을 줄여주고 모델의 너무 자유롭거나(flexible) 복잡한(overfit/complex) 성격을 줄여주는 테크닉이다. Complexity라고도 혼용되어 쓰여진다. (출처:https://velog.io/@eunice123/%EB%AA%A9%EC%A0%81%ED%95%A8%EC%88%98-%EC%86%90%EC%8B%A4%ED%95%A8%EC%88%98-%EB%B9%84%EC%9A%A9%ED%95%A8%EC%88%98-%EC%B0%A8%EC%9D%B4)

MSE는 아주 중요하므로 바로 다음에 자세히 작성할 예정이다.

• 손실함수(Loss Function)
  Loss function
  데이터 포인트에 정의되는 펑션. 예측과 라벨링에 쓰이고 페널티 측정가능.

square loss l(f(xi|θ),yi)=(f(xi|θ)−yi)2, used in linear Regression
hinge loss l(f(xi|θ),yi)=max(0,1−f(xi|θ)yi), used in SVM
0/1 loss l(f(xi|θ),yi)=1⟺f(xi|θ)≠yi, used in theoretical analysis and definition of accuracy
[5] 분류 오류가 있는지 알아볼려면 sign(f(x))이 y가 아닌 시간에대한 분수를 구하면 되는데 이는 결국 둘을 곱했을때 음수가 되는 경우를 말해서 sign(f(x))*y<0 라고 표현할 수 있고, yf(x) < 0와 yf(x)>0를 나눠서 재 분류하게되면 이게 바로 마진에 대한 분류가 되고 yf(x)<0 대해 페널티를 주는것도 가능해진다. 이때 1,0로만 페널티를 주는것도 가능하지만 다른 손실함수들을 대입해 convex 하게 표현 할 수도 있음.

출처:https://velog.io/@eunice123/%EB%AA%A9%EC%A0%81%ED%95%A8%EC%88%98-%EC%86%90%EC%8B%A4%ED%95%A8%EC%88%98-%EB%B9%84%EC%9A%A9%ED%95%A8%EC%88%98-%EC%B0%A8%EC%9D%B4)

라고는 하나, 너무 무슨 소리를 하는건지 도통 모르겠어서 다른 글을 찾아 보니,
비용함수는 모든 데이터를 받아 한꺼번에 오차를 계산, 손실함수는 각각의 데이터를 따로 오차를 계산하는 방식으로 손실함수를 Σ로 나타내면 그게 비용함수라고 한다.

이 외 오차함수(Error Function)라는 것도 있는 듯 하다.

본격적으로 머신러닝의 메커니즘을 이해하러 가보자.
딥러닝은 머신러닝의 하위 개념이라 이 선형 회귀, 그리고 나중에 후술할 로지스틱 회귀 등 똑같이 원리가 적용되므로 반드시 알아둘 필요가 있다.

시험 공부하는 시간을 늘리면 늘릴 수록 성적이 잘 나온다, 집의 평수가 클수록 매매 가격은 비싸진다 등의 어떤 변수(수치)의 값에 따라서 특정 변수의 값이 영향을 받고 있다고 볼 수 있다. 대표적으로 1차함수의 식을 생각해 보면, y=ax+b(선형 회귀에서는 a대신 w가 쓰인다)와 같은 형태에서 x는 독립적으로 변할 수 있으므로 독립 변수, y는 x에 따라 종속적으로 값이 결정되므로 종속 변수라고 한다. 선형 회귀는 바로 이 x와 y의 선형 관계를 모델링하는 것이다. 이 때 x, 즉 독립 변수가 1개라고 한다면 단순 선형 회귀, 그 이상이라면 다중 선형 회귀라고 한다. 상술했던 집의 가격은 집의 평수 뿐만 아니라 언제 지어졌는지, 방 개수는 몇개인지, 지하철 역과의 거리는 몇인지 등 다양한 요소에 따라 결정되므로, x도 여러개이다. 이런 경우 다중 선형 회귀를 이용할 수 있다.

더 직관적으로 이해하기 위해, 하나의 예시를 가져왔다.

출처ㅣhttps://wikidocs.net/21670

위 그림을 보면 점과 선이 여러개 그려져 있다. x값은 hours뿐이므로 단순 선형 회귀의 예시이다. 얼마나 공부했느냐에 따라 점수가 달라지는지, hours와 score의 관계를 가장 잘 나타내 줄 만한 직선을 찾아내는 게 바로 선형 회귀이다.
머신러닝에서는 x와 y의 관계를 유추하기 위해 H(x)=wx+b와 같은 식을 세우는데, 이러한 식을 가설이라고 한다. H는 가설(Hypothesis)의 약자이다.
이 직선은 결국 w와 b값에 따라 결정되는 것이므로, 적절한 직선을 찾아내는, 즉 적절한 w값과 b값을 찾아내는 것이 선형 회귀에서 해야 할 일이 되는 것이다.
적절한 w와 b를 찾았다면, 위 그림에 나타나 있지 않는 6시간, 7시간 혹은 그 이상의 공부를 했을 때 대략 점수가 어느 정도가 나올 것인지 예측할 수 있게 될 것이다.

x = 신호(입력값)이라 하고, 영어로는 input이라고 함
w = 가중치라 하고, 영어로는 Weight라고 함(약자)
b = 편향이라 하고, 영어로 Bias라고 함(약자)
f = 활성화 함수라 하고, 영어로 Activation Function이라고 함

뉴런(노드)으로부터 전달받은 신호 x가, 시냅스에서 가중치 w가 곱해져서, 이것이 cell body로 들어간다. cell body에서 가중치가 곱해진다고 하는 글을 봐서 헷갈렸는데, 전자가 맞는 것이다. 이렇게 각기 뉴런과 시냅스를 거쳐 들어온 x*w의 값들이 cell body에 모여 전부 합쳐지고(가중합,sum), 이 합쳐진 값에 편향인 b값이 더해진다.
이렇게 더해진 값들은 활성화 함수를 거쳐 출력값(output)이 되어 나간다.

라는 것이 퍼셉트론의 기본 이론이라는 것은 알았는데, 왜 굳이 가중치와 편향 값을 더하는 것인지? 의문이 들어, 열심히 구글링 해 본 결과 https://jh2021.tistory.com/3 이 분의 글이 정말 명확하고 알기 쉽게 설명해 주고 있다. 데이터들마다 중요도가 모두 같을 리 없기 때문에, 중요도의 정도에 따라 w를 달리 해주어야 하고, 데이터들마다 각기 성향 또한 다르기 때문에 b값을 달리 해주어야 한다.

또한, 활성화 함수를 사용하는 이유에 대해서는 https://syj9700.tistory.com/37 이 분의 글이 도움이 되었다.
활성화 함수에 대한 자세한 내용은 다음 글에 작성하는 걸로.